A Curtate Cycloid

 

Imagine a circle of radius a rolling in the positive direction on the x-axis.  A point on the circle traces a curve called a cycloid.  A point inside the circle but not at the center traces a curve called a curtate cycloid.  For example, suppose that a bicycle has a reflector attached to the spokes of its wheels.  As the bicycle moves, these reflectors trace a 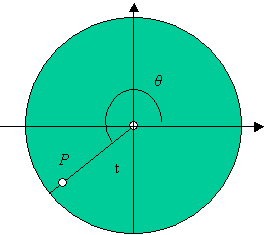curtate cycloid.

 

Let’s find parametric equations for a curtate cycloid traced by a point P located b units from the center and inside the circle.  As a first step we shall find parametric equations for the point P relative to the center of the circle ignoring for the moment that the circle is rolling along the x-axis.  Let t represent the angle through which the radius containing P has rotated assuming that P is directly below the center of the circle in the beginning, and let  represent the standard angle between the positive x-axis and the radius containing P.   Then P has coordinates  

To complete the problem, we need only find the coordinates of the center of the circle in terms of t.  The horizontal distance traveled by the center of the circle is equal to the arc length along the circle form the lowest point to the point at the end of  a radius passing through P.  This distance is equal to ta, and this is the x-cooordinate of the circle.  Thus, the center of the circle, in terms of t, is  and the point P is located at .  Finally, the parametric equations for the curve are

 

 

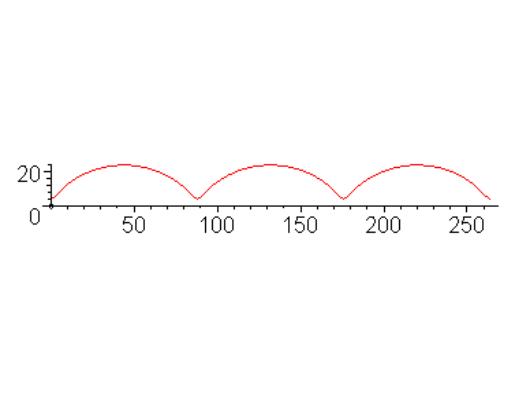
Letting  and , a Maple produced the following plot of the curtate cycloid where the units are given in inches.

Exercises

1. Suppose that
   
   .  Can the same parametric equations be used?
2. Suppose a bicycle wheel of radius a rolls along a road with equation
   
   .   Find parametric equations for the curve traced by a point b units from the center of the wheel and inside the wheel.